Справочник «Органическое вещество
Азовского моря и
прилегающих районов Чёрного моря»

Работа выполнена в рамках проекта РФФИ №15-05-08547 Долговременные изменения первичной продукции и биогеохимической трансформации органического вещества в экосистеме Азовского моря под действием природных и антропогенных факторов в 1950-2014 гг.

Ссылка на статью:
Дашкевич Л.В., Бердников С.В. Математическое моделирование температурного режима и тепловой баланс Азовского моря // Экологический вестник научных центров Черноморского экономического сотрудничества. 2008. N 4. С. 5-18.

Температура воды

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНОГО РЕЖИМА И ТЕПЛОВОЙ БАЛАНС АЗОВСКОГО МОРЯ

На основе рассмотренной в работе математической модели температурного режима Азовского моря рассчитана динамика температуры воды и элементов теплового баланса за период 1920-2008 гг. Проведено сравнение полученных результатов с литературными источниками и первичными данными из базы данных Южного научного центра РАН. Показано, что модель адекватно отражает изменения температурного режима и теплового баланса, наблюдаемые тенденции снижения солености, потепления климата, усиления циклонической деятельности, увеличения количества осадков и снижения ветровой активности в азовском регионе в современный период.

---

Моделирование климатических изменений стало едва ли не основным исследовательским методом в XXI веке. При этом далеко не всегда для оценки реальных эффектов используется база данных, собранная в экспедициях за длительный период времени.

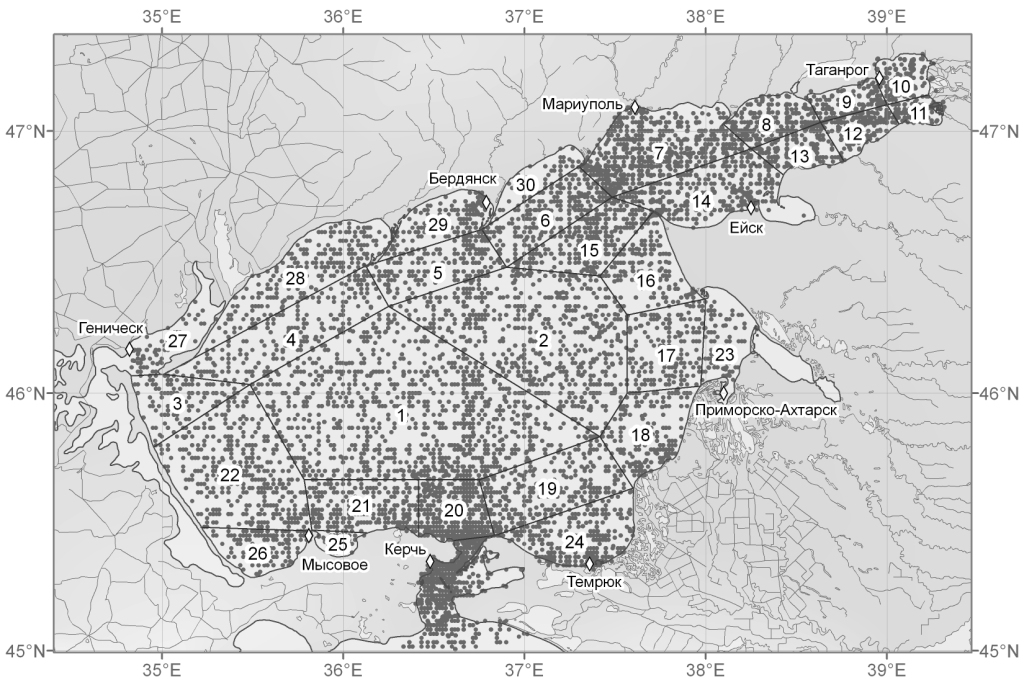
В 2005 г. Южный научный центр РАН, Мурманский морской биологический институт КНЦ РАН совместно с Лабораторией морского климата Национального центра океанографических данных (НОАА, США) начали работу по формированию базы данных океанографических наблюдений в Азовском море. Результатом стало издание Климатического атласа Азовского моря 2006 (Matishov at al., 2006), который содержал первичные данные по 14289 станциям. В 2006-2007 гг. работа по поиску и архивации данных была продолжена, подготовлена новая версия базы данных, представленная в Климатическом атласе Азовского моря 2008 (Matishov at al., 2008), которая содержит 34517 морских станций и 89203 наблюдений на береговых постах за период 1891-2006 гг. (в соответствии с рисунком 1, таблицей 1).

Таблица 1 – Перечень гидрометеорологических и гидрохимических параметров в океанографической базе данных Азовского моря за период 1891-2006 гг.

Характеристики водной среды	Число измерений*
температура	34517/89203
соленость	16724
хлорность	6711
давление	545
электропроводность	499
абсолютное содержание растворённого кислорода	8142
относительное содержание растворённого кислорода	2694
рН	3523
окисляемость кислорода	1110
фосфаты	4180
общее содержание фосфора	370
нитраты	624
нитриты	1699
аммонийный азот	258
силикаты	2090
щелочность	3315
состояние моря	10453/415
тип волнения	2653
направление волнения	9259
прозрачность	16841/39
ледовитость	24
тип льда	65
толщина льда	172/6
сплоченность льда	34
абсолютная влажность	3221
относительная влажность	3166/25008
атмосферное давление	2412
температура воздуха	11221/31421
общая облачность	10020/25400
тип облачности	2181
скорость ветра	18010/29926
направление ветра	18785/28348
видимость	3428
погода	321/1435

Примечание: *- в числителе указано количество измерений в море, в знаменателе – на береговых постах.

Для расчета температуры воды Азовского моря в рамках боксовой модели гидрологического режима предложена математическая модель, основанная на уравнениях теплового баланса. С ее помощью для трех типов лет, которые можно характеризовать как средние, теплые и холодные, выполнен расчет температурного и ледового режимов Азовского моря (Матишов и др., 2006).

Цель настоящей работы – верификация разработанной модели температурного режима для периода, наиболее обеспеченного данными (1920-2006 гг.) и совместный анализ (данных наблюдений и модельных траекторий) многолетних тенденций изменения температурного и ледового режимов, элементов теплового баланса моря.

Материал и методы

База данных (БД) ЮНЦ РАН содержит почти 120 тыс. океанографических и гидрологических станций за период c 1891 года по настоящее время (литературные данные, Интернет - ресурсы и материалы экспедиционных исследований ЮНЦ РАН и АФ ММБИ), с информацией по гидрологии, гидрохимии и метеорологии, а также численности, биомассе и видовом составе гидробионтов (всего почти 100 параметров). Все данные можно разделить на две большие категории: регулярные наблюдения на прибрежных гидрометеорологических станциях (ГМС) и экспедиционные материалы. Температура воды – самый многочисленный параметр в БД. Недостатком имеющихся данных является их не регулярное распределение во времени и пространстве, что затрудняет необходимое для климатологического анализа осреднение. Имеются значительные разрывы во временном ряде наблюдений, которые пока не удалось заполнить. Наиболее обеспечены данными периоды 1926-1935 гг., 1946-1960 гг., 1970-1980 гг. и 1998-2007 гг. Для прибрежных ГМС есть данные только для отдельных лет (1937-1939 гг., 1950-1954 гг., 1958 г., 1969-1971 гг., 1974-1975 гг.), в основном это температура поверхностного слоя и метеорологические параметры.

Для работы с БД с применением современного программного обеспечения разработана компьютерная система, включающая три взаимосвязанных блока (модуля):
1) собственно океанографическую базу данных;
2) комплекс программ для работы с табличной информацией;
3) ориентированный на современные географические информационные системы (ГИС) комплекс программ для обработки пространственно-распределенной информации.

Информация в БД хранится в виде традиционных порейсовых массивов («in situ»). К сожалению, для ряда данных, полученных из разных источников, часть признаков (например, название рейса) утрачена. В этом случае данные формируются в пределах периода относительно непрерывных наблюдений. Также в пределах нескольких месяцев (года) формируются данные прибрежных наблюдений ГМС.

Программа, обеспечивающая работу с БД, реализована в среде Access 2000. Пространственная привязка данных осуществляется с помощью ГИС ArcGIS 9.2 на батиметрической карте Азовского моря. Поскольку ГИС предоставляет возможность работы с базами Access, то такая интеграция позволяет использовать широкий набор инструментов пространственного анализа ГИС для работы с данными.

Модель температурного и ледового режимов Азовского моря встроена в гидрологический модуль боксовой модели Азовского моря, который кроме этого включает балансовые модели водного обмена и режима солености.

Горизонтальное районирование водного объекта, деление его на районы (боксы) (в соответствии с рисунком 1) проводится с целью выделения главных океанографических черт морской системы - структуры водных масс, особенностей циркуляции вод, рельефа берегов и дна, устойчивых закономерностей пространственного распределения океанографических полей, проявляющиеся на осредненных картах. Всего выделено 30 районов.

Оценка водного обмена между боксами основана на следующем уравнении водного баланса (1):

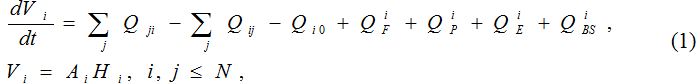
где i, j – номера районов; V_i, A_i, H_i – объем, площадь и средняя глубина, соответственно; Q_ji – приток воды из j-го района в i-й; Q_ij - отток воды из i-го района в j-й; Q_i0 - отток воды в Черное море; Q_Fⁱ - речной сток; Q_Pⁱ - осадки; Q_Eⁱ - испарение; Q_BSⁱ - поступление водных масс из Черного моря.

Водообмен за определенный период через границу, например между i-м и j-м районами, разделен на адвективную составляющую и перемешивание – водный поток, имеющий противоположное направление и одинаковую величину (2).

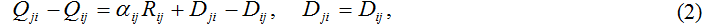
Здесь R_i - общий поток, вытекающий за определенный промежуток времени из i-го района, α_ij - его доля, направленная в j-й район. Если обозначить через α_i0 – часть потока, направленного за пределы водоема, то Q_i0 = α_i0R_i , при этом справедливо ∑ _jα_ij + α_i0 = 1. Такое упрощение позволяет заменить балансовые соотношения (1) системой линейных уравнений (3) относительно величин R_i.

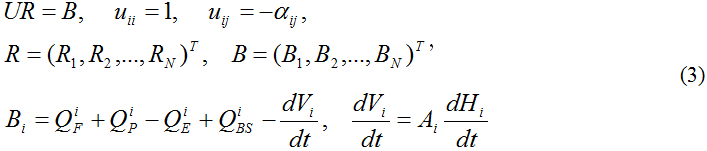
Изменение объема районов (dV_i /dt) считается известной функцией времени и отражает сезонную и межгодовую динамику изменения уровня (dH_i /dt).

Особенности водообмена между районами в разные временные периоды регулирует матрица U (т.е. значения параметров α_ij), которая может быть изменена в зависимости от преобладающего характера течений.

В результате решения системы уравнений (3) выполняется согласование имеющихся представлений о циркуляции водных масс (параметры водообмена α_ij, α_i0) и экзогенных характеристик (пресный сток, осадки, испарение, поступление черноморских вод через Керченский пролив).

Для уточнения параметров водообмена между районами уравнений водного баланса недостаточно, так как водные потоки, имитирующие горизонтальное перемешивание водных масс, не влияют на баланс воды (т.е. D_ji = D_ij ) и из уравнений исключаются. Поэтому одновременно с уравнениями водного баланса рассматриваются также балансовые соотношения для веществ, обладающие консервативными свойствами и играющими роль трассеров для маркировки перемещения водных масс. Для Азовского моря в качестве трассера используется сумма ионов (соленость, ‰). Уравнения баланса для описания динамики таких веществ имеют вид (4):

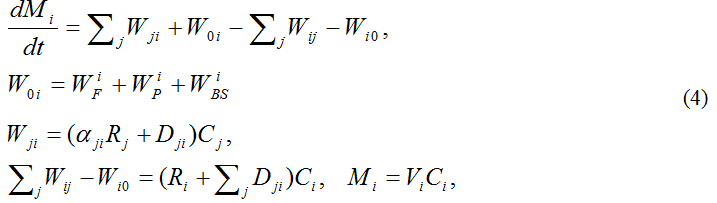
где C_i - средняя по району концентрация вещества-трассера; M_i – его запас; W_ji, W_ij - потоки вещества при перемещении водных масс между районами (адвекция и перемешивание); W_0i - экзогенное поступление вещества (с речными водами, с осадками и из Черного моря, соответственно, так как концентрация солей в осадках и речных водах незначительна, то значение имеет только поступление солей (в концентрации Cⁱ_BS) с черноморскими водами, в этом случае F_i = Qⁱ_BSSⁱ_BS); W_i0- вынос вещества с водными массами в Черное море.

Водные потоки, введенные для имитации перемешивания (ветровое перемешивание, сгонно-нагонные явления) и исключенные из уравнений водного баланса, в уравнениях баланса вещества-трассера должны быть учтены. Для их параметризации применяется такой подход D_ij: D_ji = D_ij = D₀(t)δ_ijA_ij, где D₀(t) - средняя для всего водоема, но зависящая от времени (сезона), скорость горизонтального перемешивания, δ_ij – безразмерный параметр для локальной корректировки интенсивности перемешивания; A_ij - площадь границы между районами.

Балансовые соотношения (4) представляют собой систему линейных дифференциальных уравнений (5):

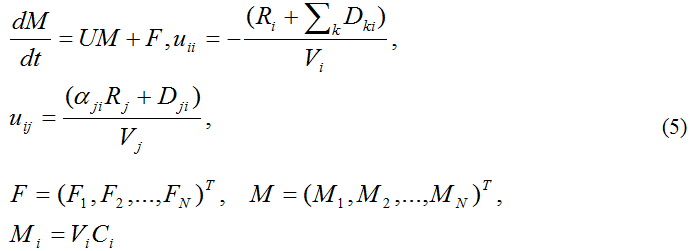
Процедура калибровки параметров модели водообмена состоит в проведении ряда вычислительных экспериментов по расчету солености с применением модели (1-5), сравнении результатов расчета с данными наблюдений, осредненными по каждому компартменту и за соответствующий период, корректировке параметров α_ij и D_ji до тех пор, пока разница между расчетными значениями и данными не будет меньше некоторой величины, принятой в качестве удовлетворительной точности модельного приближения.

Изменение запаса тепла в каждом районе в результате водного обмена между ними и притока тепла с водными массами извне описывается следующим вариантом системы уравнений (4):

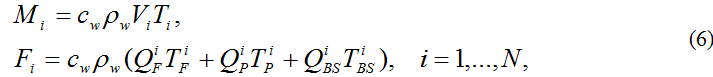
где: 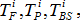- температура речной воды, осадков и водных масс, поступающих из Черного моря, соответственно (⁰K); ρ_w - плотность воды (г/см³); c_w = 4.2*10^-3 - теплоемкость воды (кДж/г/град).

Для решения системы уравнений (4)-(6) в интервале (t+dt) используется численный метод, предложенный в работе В.В. Селютиным (Матишов и др., 2006). При этом получаем оценку изменения солености (Δ_advS_i) и температуры воды Δ_advT_i в результате адвекции и перемешивания водных масс (7):

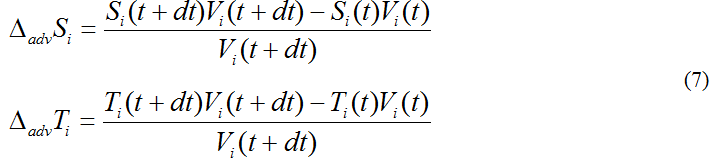
Здесь V_i(t+dt), V_i(t) - объемы районов до и после расчета, аналогично S_i(t+dt), S_i(t)- соленость, T_i(t+dt), T_i(t) - температура воды.

Значения температуры воды и солености на следующем временном шаге определяются с учетом влияния водообмена, обменных процессов с атмосферой, фазовых переходов в системе "вода-лед" следующими соотношениями (8):

а) для участков без льда (номер района здесь и далее опущен):

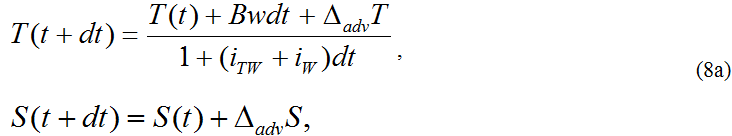
б) для участков, покрытых льдом:

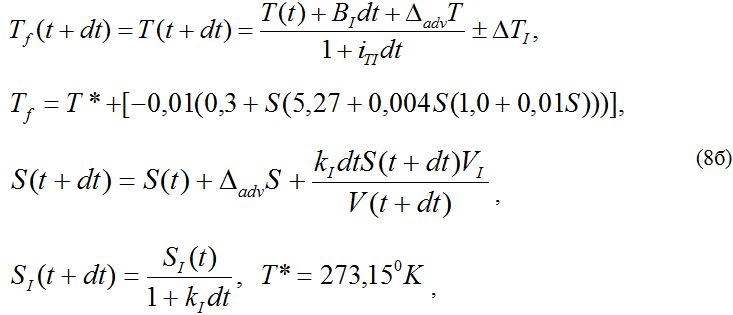
где T, S - соответственно, температура (⁰K) и соленость (‰) воды; SI - средняя соленость (‰) льда; B_w , B_i - изменение температуры за счет притока тепла к водной поверхности, свободной ото льда и покрытой льдом, соответственно; i_TW, i_TI - интенсивности уменьшения температуры воды за счет турбулентно-конвективного (контактного) теплообмена в районах, соответственно, свободных ото льда и покрытых льдом; i_W - интенсивность уменьшения температуры воды за счет теплового излучения водной поверхности; k_I - скорость выхода солей из льда; V_I – объем льда (км3); T_f.- температура замерзания морской воды (Винников, Проскуряков, 1988); ΔT_I - потоки тепла, выраженные в единицах изменения температуры воды, связанные с процессами образования и таяния льда.

Остановимся более подробно на параметризация потоков тепла через границу «вода-лед-атмосфера». Изменение температуры за счет внешнего притока тепла к поверхности воды, свободной ото льда, определяется поглощенной частью суммарной солнечной радиации (G_S), противоизлучением атмосферы (G_A), притоком тепла при турбулентно-конвективном теплообмене (G_TW), затратами тепла на испарение (G_E).

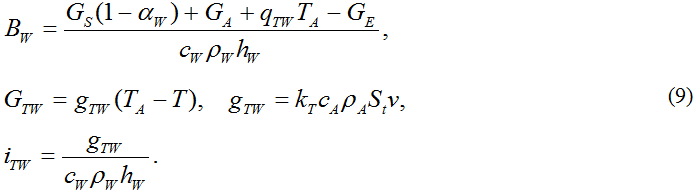
Здесь α_W - альбедо воды; T_A - температура воздуха (⁰K); k_T = 2,592*10⁶ (с/мес); c_A=1,0*10^-3- теплоемкость воздуха (кДж/г/град); ν - скорость ветра (см/с); S_t = 1,7*10^-3 - постоянная Стентона; ρ_A = 1,23*10^-3 - плотность воздуха (г/см3).

Противоизлучение атмосферы задано полуэмпирической формулой Брента (Краус, 1976):

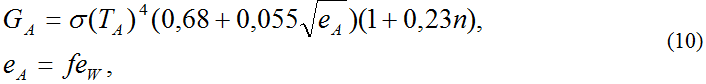
где σ =1,47*10^-8 - постоянная Стефана-Больцмана (кДж/см²/мес/град⁴), n-балл облачности (доли 1), e_W(T_A) - давление насыщенного водяного пара на высоте 2 м от поверхности воды при температуре воздуха (T_A), рассчитывается по формуле, приведенной, например в (Макштас, 1984), f - относительная влажность воздуха (доли 1).

Затраты тепла на испарение рассчитывается по формуле (Винников, Проскуряков, 1988):

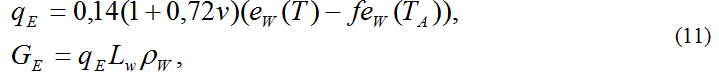
где q_E – слой испарившейся воды, мм/сут, e_W(T) - давление насыщенного водяного пара на уровне поверхности воды, ν - скорость ветра (м/с), L_w = 2,55 - скрытая теплота парообразования (кДж/г).

Изменение температуры за счет внешнего притока тепла к поверхности воды, покрытой льдом, зависит только от притока тепла за счет турбулентно-конвективного теплообмена через лед (G_TI).

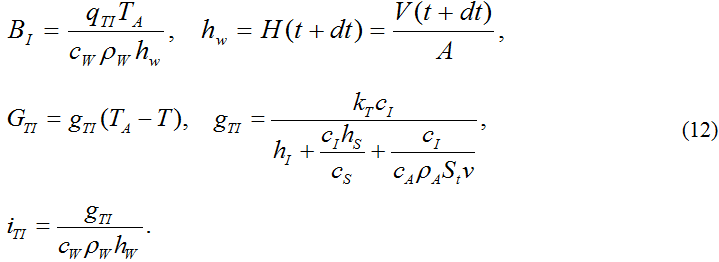
где c_I = 2,09 - теплопроводность льда (Вт/м/град); c_S = 0,31- теплопроводность снега (Вт/м/град); h_I - толщина льда (см); h_S - толщина снега (см).

Тепловое излучение водной поверхности (G_W) рассчитывается по формуле:

где δ_W = 0,91 - коэффициент серости для воды, остальные обозначения введены выше.

Динамика льда описывается двумя макрохарактеристиками - толщиной и ледовитостью (доля площади района, занятая льдом). В основу модели ледового режима положен кибернетический подход, когда процессы таяния или замерзания льда сверху, снизу или сбоку реализованы в виде последовательно выполняемых шагов общего алгоритма расчета толщины льда и ледовитости (Матишов и др., 2006).

Для расчета температурного и ледового режимов в качестве внешних факторов используются суммарная солнечная радиация, температура и относительная влажность воздуха, облачность, скорость ветра, температура речных и черноморских вод. В качестве основы использовались материалы наблюдений прибрежных гидрометеорологических станций (ГМС), а также информация из БД (в соответствии с таблицей 1).

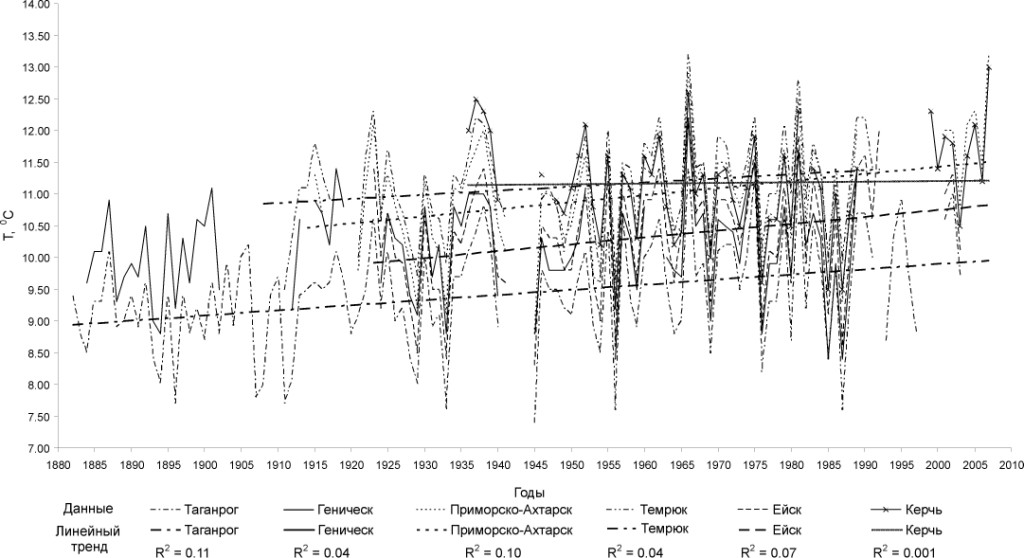
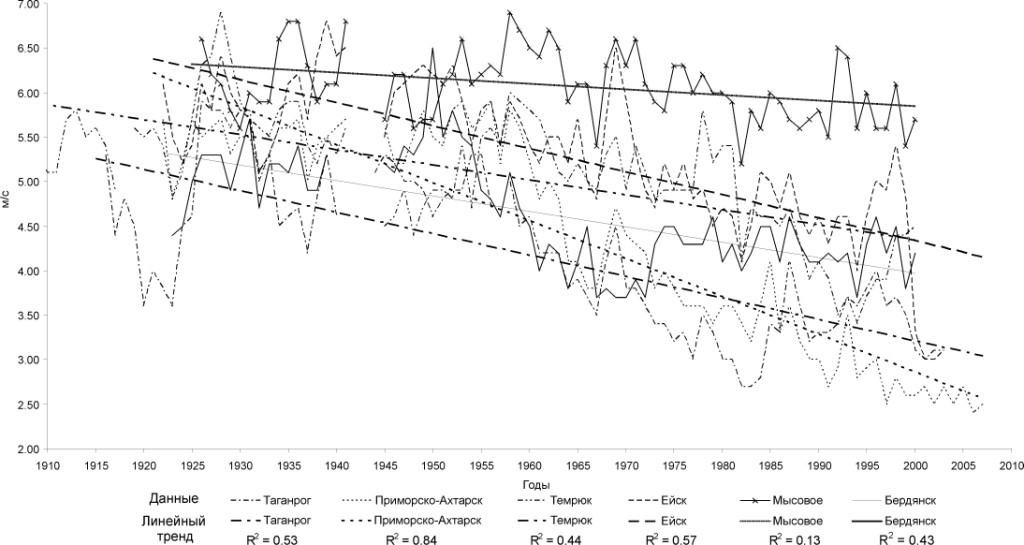
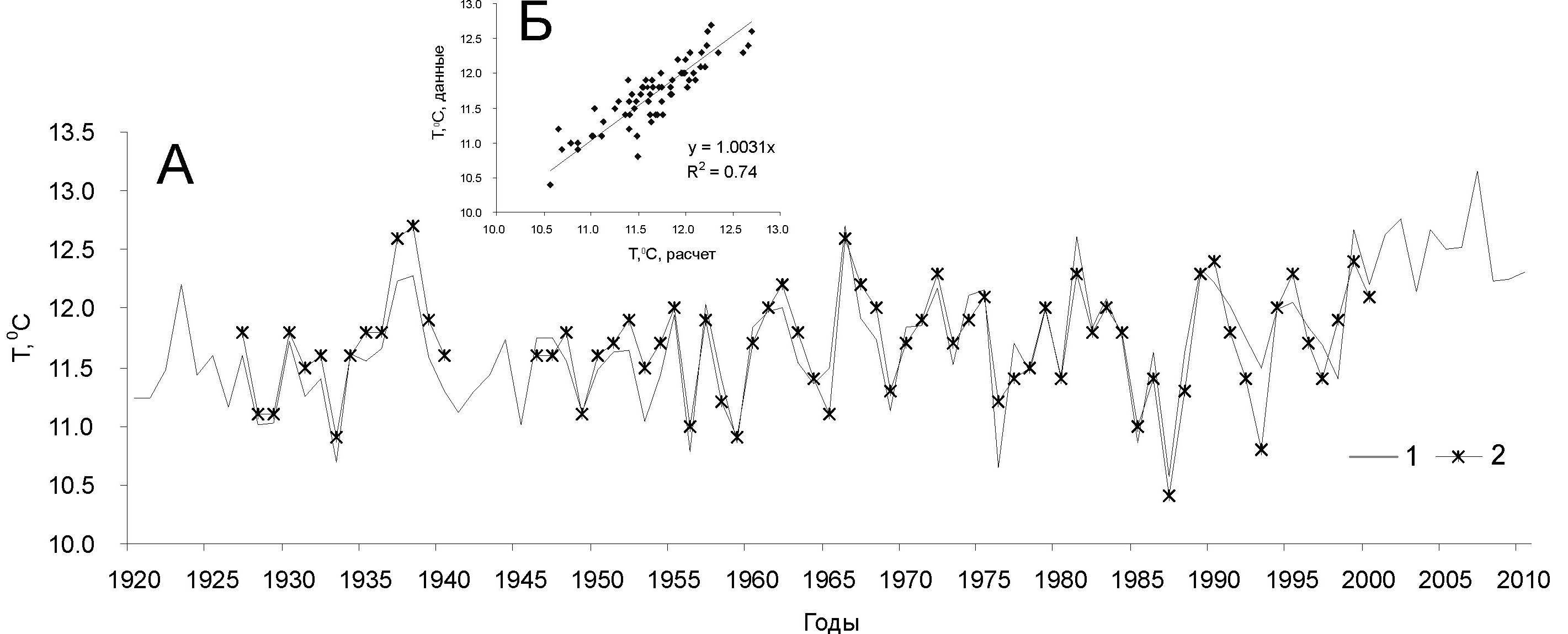
Для температуры воздуха отмечается тенденция повышения (рв соответствии с рисунком 2), а для скорости ветра – снижения (в соответствии с рисунком 3) со сменой направления преобладающих ветров с восточной на западную составляющую (Дьяков, 2002; Гаргопа, 2003; Матишов и др., 2008).

Результаты и обсуждение

Верификация модели температурного режима заключалась в корректировке ряда параметров, в частности, для затрат тепла на испарение, рассчитываемых по формуле (11), пришлось ввести коэффициент 0,8 (в работе (Трубецкова, Филимонова, 2006) также отмечается, что эта формула дает завышенные значения), необходимо было также уменьшить тепловое излучение водной поверхности (коэффициент 0,9) и увеличить на 20% противоизлучение атмосферы, рассчитываемое по формуле (10). Для сравнения использовались оценки среднегодовой температуры воды по 6 ГМС из работы (Гаргопа, 2003). Между расчетной среднегодовой температурой воды и этими данными коэффициент корреляции равен 0,86 (в соответствии с рисунком 4).

Кроме этого, полученные результаты сравнивались со справочной информацией из литературных источников (Гидрометеорологический справочник…, 1962; Гидрометеорологические условия…, 1986; Гидрометеорология и гидрохимия…,1991) и первичными данными из БД, обобщенными в работе (Matishov at al., 2008).

Данные сезонного хода температуры воды в (Гидрометеорологические условия…, 1986) и (Гидрометеорология и гидрохимия…,1991) идентичны, поэтому на рисунках представлена одна кривая для этих источников. Данные для января и февраля по акватории Таганрогского залива (ТЗ) в (Гидрометеорологический справочник…, 1962) отсутствуют, а в (Гидрометеорологические условия…, 1986; Гидрометеорология и гидрохимия…,1991) не приведены данные для января-марта по ТЗ и собственно моря (СМ), и в декабре по ТЗ, поэтому в этот период сравнение результатов расчета можно было провести только с информацией из (Matishov at al., 2008) (в соответствии с рисунком 5). Сезонный ход температуры воды в ТЗ по результатам расчета (в соответствии с рисунком 5А) смещен примерно на месяц с марта по июнь и на пол месяца и меньше во вторую половину года при сравнении с кривыми из источников (Гидрометеорологический справочник…, 1962; Гидрометеорологические условия…, 1986; Гидрометеорология и гидрохимия…,1991). При этом с кривой, построенной по данным (Matishov at al., 2008), наблюдается почти полное сходство в феврале-марте, далее расхождение аналогичное прочим источникам. Максимум температуры воды наблюдается в июле для всех кривых, при этом значения максимума расчетных данных соответствуют (Гидрометеорологический справочник…, 1962), а в остальных работах температура на 1.5-2ºС ниже.

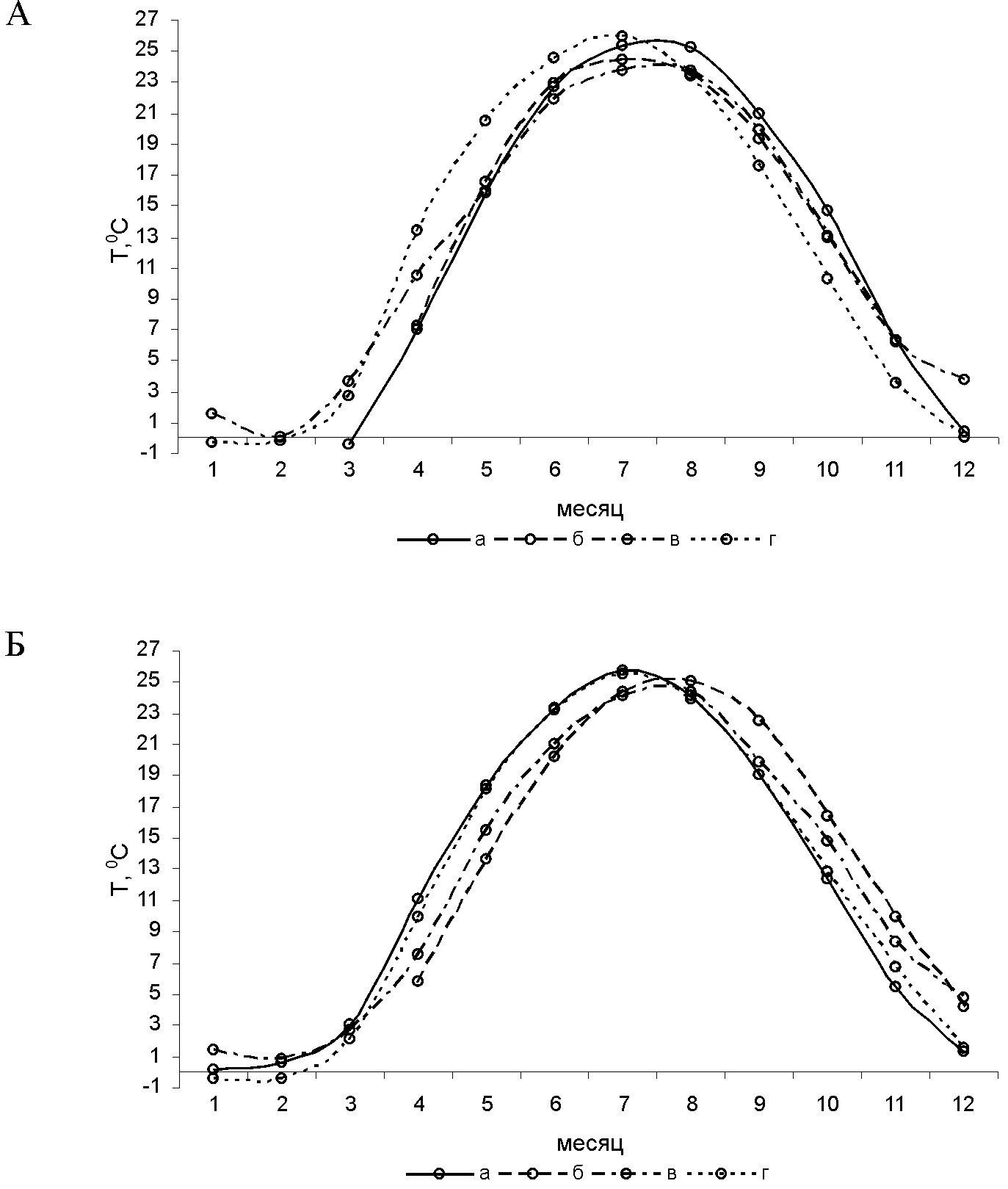
Результаты расчета сезонного хода температуры воды для СМ (в соответствии с рисунком 5Б) практически идентичны данным сезонного хода работы (Гидрометеорологический справочник…, 1962 с небольшой разницей в холодный период (результат расчета на 0,5-1ºС ниже). Кривые остальных источников – смещены вправо, т.е. имеют более плавный переход между холодным и теплым периодами, чем данные нашего расчета и работы (Гидрометеорологический справочник…, 1962), максимум температуры в них на 1-2ºС ниже и отмечается в августе (в отличие от результатов нашего расчета и работы (Гидрометеорологический справочник…, 1962), где максимум приходится на июль). Таким образом, для модели по сравнению с литературными данными характерны более высокие темпы нагревания весной и охлаждением с наступлением календарной осени.

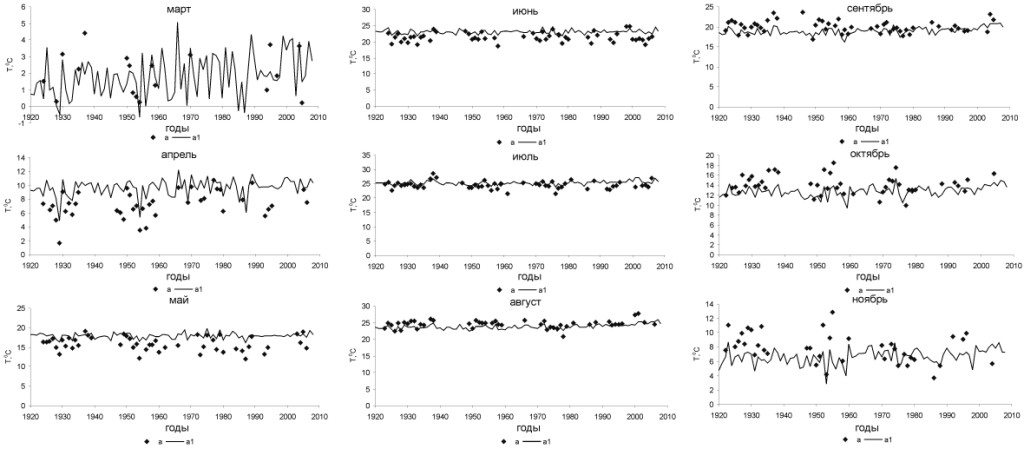
Однако, при сравнении многолетней динамики расчетной температуры с натурными данными из БД, осредненными в пределах месяца (в соответствии с рисунком 6), модель показывает хорошее соответствие. В летний сезон и в начале осени (сентябрь) наблюдается максимальное соответствие расчетной и наблюденной температуры воды, результаты расчета для апреля и мая находятся несколько выше наблюденных значений, а в октябре и ноябре расчетная кривая проходит немного ниже натурных данных. В холодный период года (в соответствии с рисунком 7) данных наблюдений за температурой воды не много и практически все они относятся к безледным областям, этим можно объяснить более низкое положение расчетной кривой. Совпадение области распределения температуры для наблюденных значений и результата расчета, можно наблюдать в марте, когда ледовый покров в азовском регионе сходит на нет.

В рамках модельных расчетов была восстановлена динамика ледового режима Азовского моря (в соответствии с рисунком 7). Данных о ледовой ситуации еще меньше, чем наблюдений температуры воды в холодный сезон, поэтому ориентироваться приходится на немногочисленные публикации. Однако, при сравнении результатов расчета с исследованиями работ (Гидрометеорологический справочник…, 1962; Гидрометеорологические условия…, 1986) можно отметить, что модель адекватно рассчитывает ледовую обстановку как для суровых (1927-1928, 1941-1942, 1953-1954, 2005-2006 г. и др.) так и для мягких (1935-1936, 1937-1938, 1947-1948, 1954-1955, 2006-2007 г. и др.) зим.

По результатам расчета с середины 1980-х отмечается некоторое стабильное повышение среднегодовой температуры воды. Возможно, это связано со снижением скорости ветра в азовском регионе в современный период (наиболее ярко с 1987 года (Гаргопа, 2003; Матишов и др., 2008)). Темпы потепления в настоящее время снизились относительно периода 1960-х - середины 1980-х, увеличилась вариабельность в пространственно-временном распределении температуры воды.

Короткопериодные колебания в рядах составляющих радиационного баланса, а также метеорологических величин (температура воздуха, аномалии атмосферного давления, осадки) показывают наличие связи между атмосферными факторами и изменениями составляющих радиационного баланса (Покровский и др., 2004). Связь долговременных колебаний потоков тепла и осадков с глобальным изменением климата также отмечена в ряде исследований, поэтому было интересно проверить ее наличие для Азовского моря.

Расчет элементов теплового баланса для Азовского моря, в отличие от водного и солевого, в литературе представлен недостаточно. Удалось найти только три работы, в которых этому вопросу уделено внимание - это фундаментальные издания по гидрометеорологии Азовского моря (Гидрометеорологический справочник…, 1962) и (Гидрометеорология и гидрохимия…,1991) и статья (Спичак, 1963), также известно о работе И.Б. Славина (1965), но найти ее не удалось.

В рамках моделирования температурного режима Азовского моря был проведен расчет элементов теплового баланса и их динамики во времени для периода 1920-2008 гг. Отмечено статистически значимое снижение затрат на испарение, увеличение эффективного излучения и уменьшение радиационного баланса с течением времени. Первое вероятно связано с наблюдаемым снижением скорости ветра в азовском регионе, второе и третье – с повышением температуры и увеличением облачности.

Кроме этого, отмечен некоторый рост поглощенной радиации, что вероятно связано с наблюдаемым в последней четверти ХХ в. по данным многих актинометрических станций России отрицательным трендом альбедо в зимний период (Покровский и др., 2004), в случае Азовского моря это может быть связано с большим количеством мягких зим относительно суровых (Дьяков и др.., 2002).

Сравнение среднемноголетней годовой величины элементов теплового баланса по результатам нашего расчета с информацией, приведенной в литературе, представлено в таблице 2.

Таблица 2 – Среднемноголетние годовые значения элементов теплового баланса (МДж/м²)

Параметр	Район	Источник
		Данная работа	(Гидрометеорология и гидрохимия…, 1991)	(Гидрометеорологический справочник…, 1962)	(Спичак, 1963)
		Период расчета (годы)
		1920-2008	До 1986	1891-1958	1946-1960
Тепло на образование/таяние льда	СМ		±40-60	-	-
	ТЗ		±80-100	-	-
	АМ	±70		-	±58.6
Суммарная радиация	СМ		5250	-	-
	ТЗ		4850	-	-
	АМ	3350-3750	-	3559-3978	4773-5192
					-4940
Радиационный баланс	СМ	1250-1650	2700-2750	-	-
	ТЗ	1400-1700	2400	-	-
	АМ	1300-1650	-	-	2805
Эффективное излучение	СМ	1850-2400	1590	-	-
	ТЗ	1700-2200	1460	-	-
	АМ		-	1256	1465-1758
					-1675
Поглощенная радиация	СМ	3350-3750	4200-4300	-	-
	ТЗ	3300-3700	3800-4000	-	-
	АМ		-	-	4480
Затраты тепла на испарение	СМ	2100-2500	2000	2512	-
	ТЗ	2150-2550	2200-2500	1465	-
	АМ		-	1884-2303	1968-2554
					-2303
Турбулентный теплообмен между водой и атмосферой	СМ	-70…-300	-150…-200	-	-
	ТЗ	-150…-370	-520	-	-
	АМ	-	-	-126…-293	-360…-611
					(-460)

Примечание: СМ – собственно море; ТЗ – Таганрогский залив; АМ – Азовское море.

Заключение

Рассмотренная в работе математическая модель адекватно отражает изменения температурного режима и теплового баланса, наблюдаемые тенденции снижения солености, потепления климата, усиления циклонической деятельности, увеличение количества осадков и снижение ветровой активности в азовском регионе в современный период.

В результате анализа данных наблюдений и результатов расчета сделан вывод о влиянии на наблюдаемый рост температуры воды Азовского моря дополнительных факторов (кроме зафиксированного повышения температуры воздуха), а именно:

- в связи с понижением солености в современный период температура замерзания воды повысилась, что дает статистически более высокую среднегодовую температуру воды;

- уменьшение скорости ветра приводит к некоторому снижению затрат тепла на испарение, что также может способствовать повышению температуры.

- в свою очередь усиление циркуляции в азовском регионе и рост температуры воды могут влиять на снижение радиационного баланса и рост эффективного излучения.

---

1. Matishov G., Matishov D., Gargopa Yu., Dashkevich L., Berdnikov S., Baranova O., Smolyar I. Climatic Atlas of the Sea of Azov 2006. G. Matishov, S. Levitus, Eds., NOAA Atlas NESDIS 59, U.S. Government Printing Office, Washington, D.C., 2006, 103 pp., CD-ROM.
2. Climatic Atlas of the Sea of Azov 2008. G. Matishov, D. Matishov, Y. Gargopa, L. Dashkevich, S. Berdnikov, O. Baranova, I. Smolyar G.Matishov, S. Levitus, Eds., NOAA Atlas NESDIS 65, U.S. Government Printing Office, Washington, D.C., 2008, International Ocean Atlas and Information Series, V. 11, 148 pp., CD-ROM.
3. Матишов Г.Г., Гаргопа Ю.М., Бердников С.В., Дженюк С.Л. Закономерности экосистемных процессов в Азовском море. М.: Наука. 2006. 304 с.
4. Винников С.Д., Проскуряков Б.В. Гидрофизика. Л.: Гидрометеоиздат, 1988. - 247 с.
5. Краус Е. Взаимодействие атмосферы и океана. Л.: Гидрометеоиздат. 1976. - 295 с.
6. Макштас А.П. Тепловой баланс арктических льдов в зимний период. Л.: Гидрометеоиздат. 1984. - 67 с.
7. Дьяков Н.Н., Иванов В.А., Горбач С.Б. Сезонная и межгодовая изменчивость гидрологических характеристик прибрежной зоны Азовского моря // Экологическая безопасность прибрежной и шельфовой зон и комплексное использование ресурсов шельфа: Сб.науч.тр. Вып.1 (6) – НАН Украины, МГИ, ОФ ИнБЮМ, Севастополь, 2002. с. 39-46.
8. Гаргопа Ю.М. Крупномасштабные изменения гидрометеорологических условий формирования биопродуктивности Азовского моря. Дисс. Докт. Геогр. Наук., Мурманск. 2003. 467c.
9. Матишов Г.Г., Матишов Д.Г., Гаргопа Ю.М. Климатогенные изменения экосистем южных морей в условиях антропогенных воздействий // Известия РАН. Серия географическая, 2008. № 3, с. 26-34.
10. Трубецкова М.Д., Филимонова М.К. Об оценке испарения с поверхности Каспийского моря в современный период // Тр. междун. Науч. Конф. «Экстремальные гидрологические события в Арало-Каспийском регионе» (Москва, 19-20 октября 2006 г.), Москва. 2006. С. 79-84.
11. Гидрометеорологический справочник Азовского моря. Л.: Гидрометеоиздат. 1962. 853 с.
12. Гидрометеорологические условия шельфовой зоны морей СССР. Т. 3. Азовское море. Л:, 1986. 218 с.
13. Гидрометеорология и гидрохимия морей СССР. Т. V. Азовское море. - СПб.: Гидрометеоиздат. 1991. 237 с.
14. Покровский О.М., Махоткина Е.Л., Покровский И.О., Рябова Л.В. Тенденции межгодовых колебаний составляющих радиационного баланса и альбедо поверхности суши на территории России // Метеорология и гидрология, 2004, № 5. с. 37-46.
15. Спичак М.К. Элементы теплового баланса и их роль в формировании гидрометеорологического режима и первичной продуктивности Азовского моря // Рыбохозяйственные исследования в Азовском бассейне по запасам рыб и условиям их обитания, Тр. Вып. 6, изд. Рыбное хоз-во, 1963. с. 27-31.